后缀数组
后缀
对于一个串来说,第i个字符开始的串就是后缀。。。
举个栗子:对于串ababa来说,ababa、baba、aba、ba、a都是它的后缀
后缀数组
我们将后缀编号(其实就是开始的那个字符在原串中位置)然后按照字典序排序这些后缀,得到了以下顺序
- a
- aba
- ababa
- ba
- baba
可以看到后缀按字典序排名后的顺序是 5 3 1 4 2 ,我们开一个sa数组(即后缀数组),用sa[i]表示排名为i的后缀的编号(开始字符在原串中的位置)。
同时我们可以开一个rk数组,用rk[i]表示编号为i的后缀的排名。
思想
暴力
我们可以考虑$O(n\log{n})$排序后缀,但考虑单次任意比较的复杂度是$O(n)$的,所以总复杂度趋近$O(n^2\log{n})$,肯定会被大数据卡掉。
优化1:倍增
我们还是用这个例子开始排序
- ababa
- baba
- aba
- ba
- a
我们先比较这些后缀数组的第一位
- ababa
- aba
- a
- baba
- ba
然后比较它们的前两位(因为第一位已经排好,其实这里就是比较第二位)
- a
- ababa
- aba
- baba
- ba
然后比较他们的前四位(因为前两位已经排好,其实这里就是比较三、四两位)
- a
- aba
- ababa
- ba
- baba
然后发现对于这个例子已经排序完成,额,如果没有排序完成,我们需要一直这么下去。假设现在还没有完成,我们需要比较前五位(其实就是比较最大的小于n的2的次方位到第n位之间的位)
额,不好意思,这样好像没有什么用啊。。。
额。。。
我们这么处理,就会有用了。在读入字符串后,我们根据单个字符排序
(以每个后缀的第一个字符排序)
| a | b | a | b | a |
|---|---|---|---|---|
| 1 | 2 | 1 | 2 | 1 |
接着向后合并相邻字符,再次排名,我们发现a原来排名是1,b原来是2,a向b合并后是1 2,b向a合并是2 1,我们把合并后的名次排名,便成了2和3(还有一个单字符的a,其实是补零排序)
对,我们这样每次排序两个排名组成的数即可。
| ab | ba | ab | ba | a |
|---|---|---|---|---|
| a b | b a | a b | b a | a |
| 1 2 | 2 1 | 1 2 | 2 1 | 1 0 |
| 2 | 3 | 2 | 3 | 1 |
我们接着向后合并成4个字符
| abab | baba | aba | ba | a |
|---|---|---|---|---|
| ab ab | ba ba | ab a | ba | a |
| 2 2 | 3 3 | 2 1 | 3 0 | 1 0 |
| 3 | 5 | 2 | 4 | 1 |
接着合并知道合并到最大的小于n的2的次方个字符,然后最后合并到n个
| ababa | baba | aba | ba | a |
|---|---|---|---|---|
| abab a | baba | aba | ba | a |
| 3 1 | 5 0 | 2 0 | 4 0 | 1 0 |
| 3 | 5 | 2 | 4 | 1 |
好了,我们排序完了。
可以发现我们一共整体排序了$\log{n}$次,一次排序的复杂度是$O(n\log{n})$。我们发现,这样我们就把整体的复杂度降到了$O(n\log^2{n})$
最后再举一个常见的例子,希望大家看完这个后能彻底明白这个排序的过程
Example: aabaaaab
第一次
| a | a | b | a | a | a | a | b |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 1 | 1 | 1 | 1 | 2 |
第二次
| aa | ab | ba | aa | aa | aa | ab | b |
|---|---|---|---|---|---|---|---|
| a a | a b | b a | a a | a a | a a | a b | b |
| 1 1 | 1 2 | 2 1 | 1 1 | 1 1 | 1 1 | 1 1 | 2 0 |
| 1 | 2 | 4 | 1 | 1 | 1 | 2 | 3 |
第三次
| aaba | abaa | baaa | aaaa | aaab | aab | ab | b |
|---|---|---|---|---|---|---|---|
| aa ba | ab aa | ba aa | aa aa | aa ab | aa b | ab | b |
| 1 4 | 2 1 | 4 1 | 1 1 | 1 2 | 1 3 | 2 0 | 3 0 |
| 4 | 6 | 8 | 1 | 2 | 3 | 5 | 7 |
第四次
| aabaaaab | abaaaab | baaaab | aaaab | aaab | aab | ab | b |
|---|---|---|---|---|---|---|---|
| aaba aaab | abaa aab | baaa ab | aaaa b | aaab | aab | ab | b |
| 4 2 | 6 3 | 8 5 | 1 7 | 2 0 | 3 0 | 5 0 | 7 0 |
| 4 | 6 | 8 | 1 | 2 | 3 | 5 | 7 |
排序完成
上面的过程用图表示为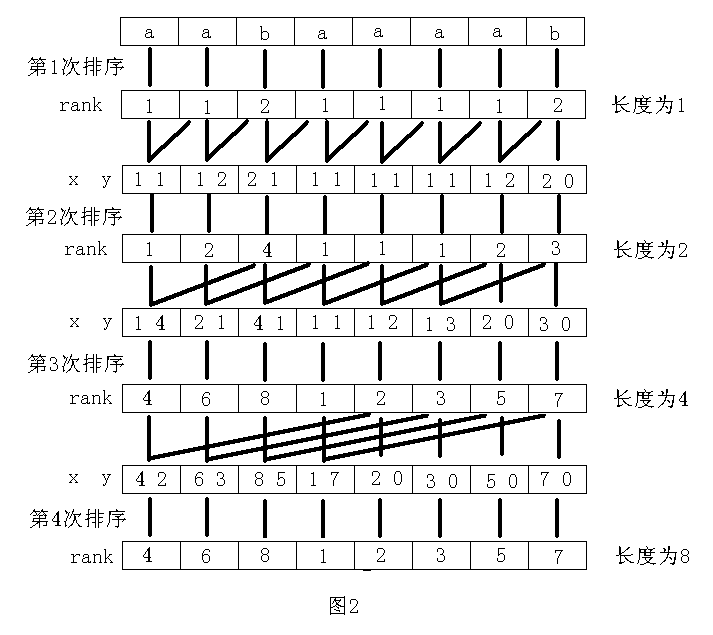
优化2:基数排序
如果我们用快排的话还是太慢,考虑到每一次排序我们都是在排两位数,所以我们用基数排序优化一下可以将排序优化到$O(n)$,这样总复杂度就降到了$O(n\log{n})$
怎么基数排序?
建两个桶,一个用来装个位排序,一个用来装十位排序,我们每次先把数加到个位桶里排序,再加到十位桶排序,这样就可以保证对于每一个十位桶里的数肯定是个位升序的。
实现
我们用s读入字符串,保存从s[1]到r[n],长度为n,且最大值小于m。
为了函数操作的方便,约定除s[n]外所有的s[i]都大于0,s[n]=0。
函数结束后,结果放在sa数组中,从sa[1]到sa[n]。
函数的第一步,要对长度为1的字符串进行排序。
一般来说,在字符串的 题目中,s的最大值不会很大,所以这里使用了计数排序。
如果s的最大值很大,那么把这段代码改成快速排序。
1 | for(int i=1;i<=n;i++) |
这里x数组保存的值相当于是rk值。下面的操作只是用x数组来比较字符的大小,所以没有必要求出当前真实的rk值。
接下来进行若干次基数排序,在实现的时候,这里有一个小优化。
基数排序要分两次,第一次是对个位桶排序,第二次是对十位桶排序。对十位桶排序的结果实际上可以利用上一次求得的sa直接算出,没有必要再算一次。
1 | for(int i=n-j+1;i<=n;i++) |
其中变量j是当前字符串的长度,数组y保存的是对个位桶排序的结果。然后要对十位桶进行排序
1 | for(int i=0;i<=m;i++) |
这样便求出了新的sa值。在求出sa后,下一步是计算rk值。这里要注意的是,可能有多个字符串的rk值是相同的,所以必须比较两个字符串是否完全相同,y数组的值已经没有必要保存,为了节省空间,这里用y数组保存rk。这里又有一个小优化,将x和y定义为指针类型,复制整个数组的操作可 以用交换指针的值代替,不必将数组中值一个一个的复制。
1 | swap(x,y); |
其中cmp函数的代码是:
1 | bool cmp(int *s,int a,int b,int l) |
这里可以看到规定 r[n]=0 的好处,如果 r[a]==r[b] ,说明以 r[a] 或 r[b]开头的长度为 l 的字符串肯定不包括字符 r[n] ,所以调用变量 r[a+l] 和 r[b+l]不会导致数组下标越界,这样就不需要做特殊判断。执行完上面的代码后, rk值保存在 x 数组中,而变量 p 的结果实际上就是不同的字符串的个数。这里可以加一个小优化,如果 p 等于 n ,那么函数可以结束。因为在当前长度的字符串 中 ,已经没有相同的字符串,接下来的排序不会改变 rk 值。例如说明中的第五次排序和另一个例子的第四次排序,实际上是没有必要的。
对上面的两段代码,循环的初始赋值和终止条件 可以这样写:
1 | for(int j=1;j<=n;j<<=1) |
在第一次的排序以后, rk 数组中的最大值小于 p ,所以让 m=p 。
下面是洛谷模板题的代码
1 |
|
最长公共前缀
又叫LCP问题,lcp(i,j)为suffix(sa[i])与suffix(sa[j])的最长公共前缀
性质
显而易见的,我们可以得到
- lcp(i,j)=lcp(j,i)
- lcp(i,i)=len(sa[i])=n-sa[i]+1
这两条性质可以将lcp(i,j)的三种情况变简单
- i<j 计算
- i>j 转化为lcp(j,i)即转化为i<j
- i=j 直接计算
LCP Lemma
- lcp(i,j)=min(lcp(i,k),lcp(k,j)) (对于任意1<=i<=k<=j<=n)
证明:
设p=min(lcp(i,k),lcp(k,j))则lcp(i,k)>=p,lcp(k,j)>=p
设suffix(sa[i])=u,suffix(sa[k])=v,suffix(sa[j])=w
则u和v前p个字符相等,v和w前p个字符相等
所以u和w前p个字符相等,则lcp(i,j)>=p
设lcp(i,j)=q>p则q>=p+1
p=min(lcp(i,k),lcp(k,j)),所以u[p+1]!=v[p+1]或v[p+1]!=w[p+1]
但是v[p+1]=w[p+1],自相矛盾
所以lcp(i,j)<=p
综上所述lcp(i,j)=p=min(lcp(i,k),lcp(k,j))
LCP Theorem
- lcp(i,j)=min(lcp(k,k-1)) (对于任意1<=i<=k<=j<=n)
结合LCP Lemma,lcp(i,j)=min(lcp(i,i+1),lcp(i+1,j))
而lcp(i,i+1)=lcp(i+1,i)=lcp(i+1,(i+1)-1)
lcp(i+1,j)=min(lcp(i+1,i+2),min(lcp(i+2,i+3),…))
最终可以得到用k替换i+1、i+2、…最终得到lcp(i,j)=min(lcp(k,k-1))
求法
我们设height[i]=lcp(i,i-1),1<i<=n,显然height[1]=0
由LCP Theorem得lcp(i,j)=min(height[k]) i<k<=j即i+1<=k<=j
那怎么求height[i]?
设h[i]=height[rk[i]],同样的height[i]=h[sa[i]]
一条很重要的定理:
h[i]>=h[i-1]-1
我们假设i-1的字符串排名前一位的字符串就为第j个(j=sa[rk[i-1]-1]),注意j不是第i-2个字符串。
第j个字符串和第i-1个字符串公共前缀为height[rk[i-1]]
第j+1个字符串和第i个的关系
- 第j个和第i-1个首字母不同
那么j+1极可能在i前头,也可能在i后面,没有关系,因为height[rk[i-1]]=0,无论height[rk[i]]是多少都有height[rk[i]]>=height[rk[i-1]]-1,也就是h[i]>=h[i-1]-1 - 第j个和第i-1个首字母相同
那么由于j+1是j去除首字母得到的,i也是i-1去除首字母的到的那么显然j+1排在i前,同时,第j个字符串和第i-1个字符串的最长公共前缀为height[rk[i-1]],那么显然k+1和i的最长公共前缀是height[rk[i-1]]-1
我们试想一下,对于比第i个字符串排名更靠前的那些字符串,与i最长公共前缀长度最长的肯定是与i紧邻的那个字符串,即sa[rk[i]-1]。但是我们前面求得,有一个排在i前面的字符串j+1,lcp(rk[i],rk[j+1])=height[rk[i-1]]-1
又因为height[rk[i]]=lcp(i,i-1)>=lcp(i,j+1)
所以height[rk[i]]>=height[rk[i-1]]-1,即h[i]>=h[i-1]-1
代码
1 | void get_height() |
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。
若你觉得我的文章对你有帮助,欢迎点击上方按钮对我打赏


